It’s possible to share a secret amongst a group of people so that only some of them are needed to reconstruct it…
Secrets with Friends
Why would you even want to do that?
There are plenty of use cases for splitting secrets amongst different parties - so that no individual can uncover it alone. Dead Person Switches (the topic of my dissertation) might use this technique, and could be applied to:
- Protecting a whistleblower’s secret
- Passing control of inactive accounts after death
- Distribution of wealth after death
More generally, it’s desirable to be able to distribute fragments of a secret to an arbitrary number of people, and require that a subset of them be present to reconstruct it. This is known as a K of N distribution scheme.
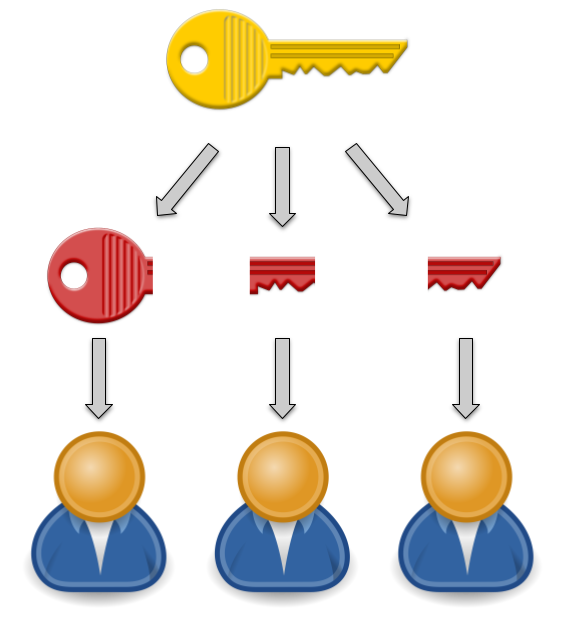
Using a K of N scheme allows us to prevent an individual from reconstructing the secret alone, but provides some resilience against a number of people being unable or unwilling to cooperate when it is time to uncover the secret.
Shamir’s Secret Sharing Scheme
Shamir’s Secret Sharing Scheme (SSSS) is a commonly used K of N threshold scheme. A secret can be divided into N fragments, of which only K are required to reconstruct it.
In 15 Men on a Dead Man’s Switch, Jameson Lopp describes a method for encrypting and storing secrets, and distributing fragments of the decryption key to a number of trusted people, using SSSS to generate the fragments.
A number of implementations of SSSS exist, including a unix tool which simplifies the process of dividing a secret into fragments. Jameson also suggests using a passphrase, and as the unix tool supports application of SSSS to secrets of up to 128 ASCII characters, this allows for the use of a strong passphrase.
How to use SSSS
You can install SSSS on your Mac using homebrew:
In the example below, SSSS is being used to split a secret, "X marks the spot", into 5 fragments:
$ ssss-split -t 3 -n 5
Generating shares using a (3,5) scheme with dynamic security level.
Enter the secret, at most 128 ASCII characters: X marks the spot
Using a 128 bit security level.
1-a07cfafadfb8c949e10043063dd77bf9
2-c8aca4294241312eae985d2480ffa9f7
3-b94432ce93edd7d2d360939fc0f4b641
4-08426b9a2a8d5f0cde7c1b33734c35bc
5-79aafd7dfb21b9f0a384d58833472a18
The secret can then be reconstituted using only 3 of them:
$ ssss-combine -t 3
Enter 3 shares separated by newlines:
Share [1/3]: 3-b94432ce93edd7d2d360939fc0f4b641
Share [2/3]: 5-79aafd7dfb21b9f0a384d58833472a18
Share [3/3]: 1-a07cfafadfb8c949e10043063dd77bf9
Resulting secret: X marks the spot
In Jameson’s example, the secret, which is fragmented using SSSS, is actually a key which can be used to decrypt something much larger.
How does it work?
SSSS relies on the notion that K points can define a polynomial curve of degree K-1.
| Points |
Polynomial curve |
Polynomial degree |
| 2 |
Line |
1 |
| 3 |
Parabola |
2 |
| 4 |
Cubic curve |
3 |
If a specific polynomial curve is the secret, then a minimum of K points are required to reconstruct the original curve, and the degree of the polynomial defines K.
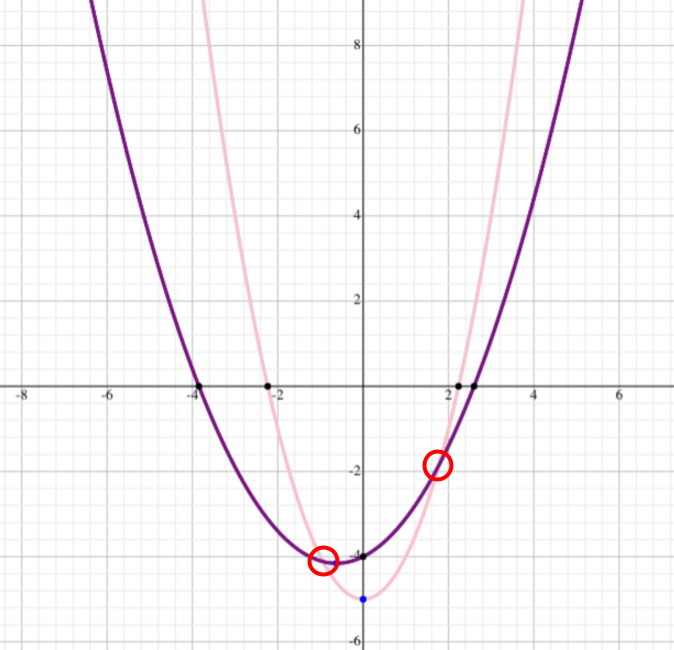
For instance, here there are 2 parabolas (polynomials of degree 2), and given only 2 points it is not possible to distinguish them (or any other number of parabolas that pass through these points). However, by providing a third point, they can be disambiguated - and only 1 parabola will match a given set of 3 points.
A subject can select N points from the curve, and give those to N trusted contacts. N can be arbitrarily large, provided it is larger than K, and so K of the N distributed points can be used to reconstruct the curve.



